We found a significant difference (p<0.05) between conditions.

If you’ve been in science for any length of time, you’ve probably written some version of this sentence. But what does p<0.05 actually mean and why does that make a difference “significant”?

Very simply, a p value indicates how likely it is that a difference between two groups is real.* The number is the percent likelihood that the two groups are the same (or that any differences between them are just due to chance). A p value of 0.95 means there’s a 95% chance the two groups aren’t different, 0.05 means there’s a 95% chance the groups are different, and 0.5 means it’s 50:50. Thus, stating that p<0.05 means that there is more than a 95% chance that the difference you’re describing is real.**

True/False Positive/Negative

A statistical test can never be 100% certain. Because of this, there’s always a chance that a) a difference with a low p value isn’t actually real (false positive) or b) a difference with a high p value is real (false negative). Of course, there is also the possibility that your statistical results were correct and you got a true positive (low p value and real difference) or a true negative (high p value and no difference). A good statistical analysis will minimize false positives/negatives while maximizing true positives/negatives.

Multiple Testing

A 95% chance of being right sounds pretty good. And it is pretty good if you’re only performing one statistical test. However, if you’re working in untargeted metabolomics (and I hope you are!), there’s no way you’re performing a single statistical test on a regular basis. Instead, you’re probably applying the same test to thousands of metabolites at once. The problem is, the more tests you perform, the higher the chance you’re going to get something wrong.

Take the graph above. As you can see, it doesn’t take very many tests to get to a point that there’s a 99% chance that one of your p<0.05 results is wrong. Performing a thousand tests? There’s a 5e-23 chance that all those results will be correct. This phenomenon is called the problem of multiple comparisons and is the basis for p-hacking, the dubious (and occasionally hilarious) practice of applying statistical tests to random data until you get p<0.05.

So what do you do? Thankfully, there are a lot of statistical tools to help minimize this issue. The simplest is the Bonferroni, which simply sets the new threshold for significance at p=0.05 divided by the number of tests you performed. Ran 20 tests? You’ll now need p=0.0025 (0.05/20) to be considered significant. Ran 1000 tests? Now your p value needs to be below 0.00005. While the Bonferroni is simple and easy to implement, it’s generally considered too stringent when you’re working with large datasets. Instead, many people prefer the Benjamini-Hochberg adjustment (also called BH or FDR), which does a better job of balancing true and false positives.

What about other metrics?

While a p value might be the most popular way to report statistical results, it’s hardly the only way. In fact, other metrics such as fold change, effect size, or confidence interval are often more useful. For instance, a p value will tell you how likely a difference between groups is real, but it won’t tell you how big that difference is or whether it’s biologically relevant. In many cases, a 2% difference with a p value of 0.0001 is less interesting than a 200% difference with a p value of 0.51.

So what should you do? First, don’t just report p values. A p value is most useful when taken in context. Use all the information you have and don’t assume your job is done just because p<0.05.

So what is this “significance”? Traditionally, many fields placed a hard cutoff at p=0.05 to deem a result significant. Anything below that mark was accepted without question, but anything above that mark (even p=0.051!) was discarded. But as Rosnow and Rosenthal famously put it, “Surely God loves the .06 nearly as much as the .05.” While p=0.05 is a perfectly fine cutoff, there is nothing magical about it. The difference between p=0.51 and p=0.49 is just the difference between being 94.9% sure and 95.1% sure that what you’re describing is real. Thankfully, many fields have started to recognize this and relaxed rules on p value cutoffs. In fact, in a few years, we may finally be done writing that first sentence.

How does this work in Ometa Flow?

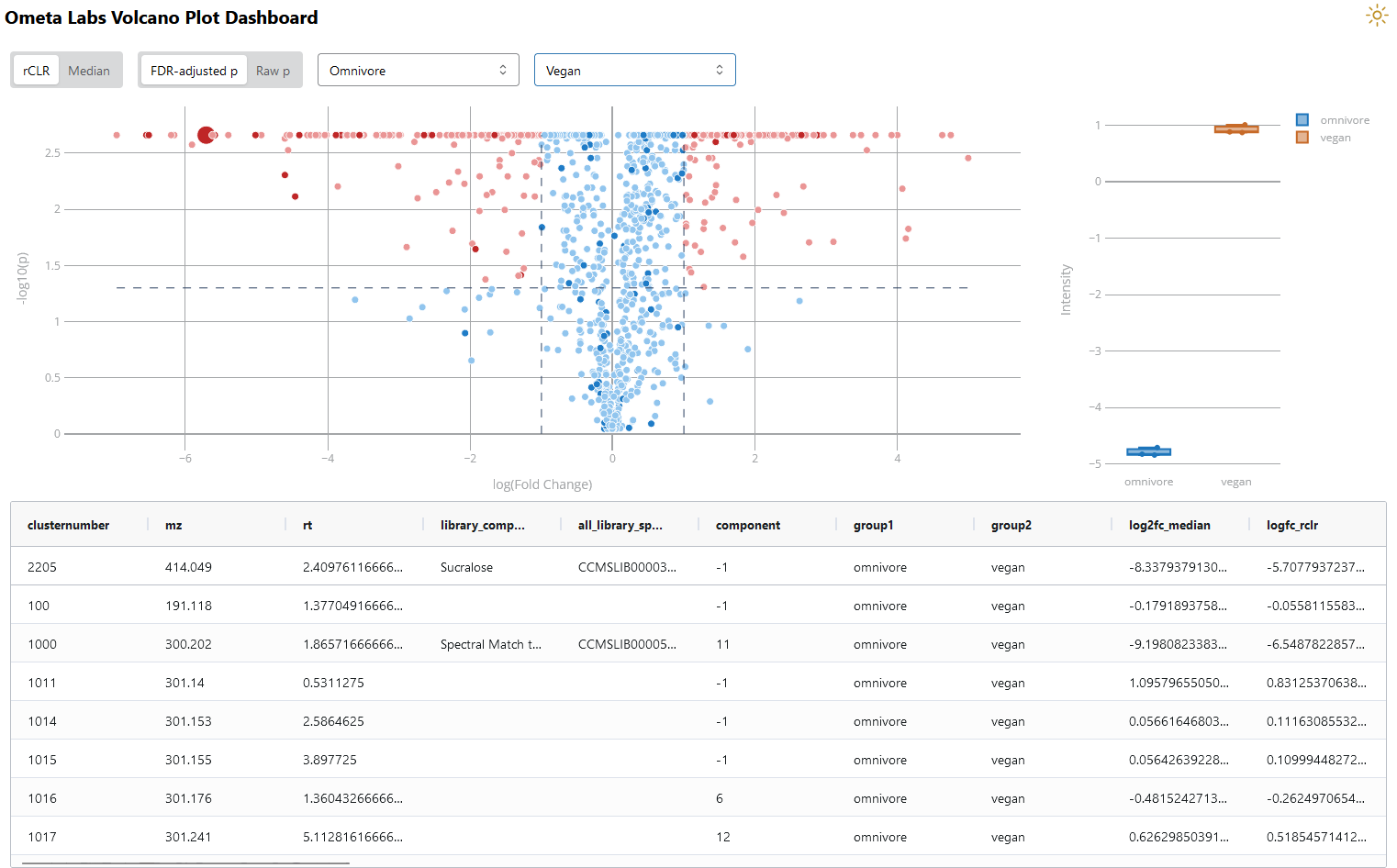
Many of the statistical tools in our new-and-improved statistics processing workflow will output a p value. One of the simplest ways to visualize these results is the volcano plot dashboard. This dashboard displays each metabolite based on its fold change and p value. Metabolites in the upper corners have both large fold changes and small p values (a good combination!). Darker points indicate which metabolites have a library annotation. The p values used in this dashboard are calculated using Tukey’s Honestly Significant Difference (Tukey’s HSD), which corrects for multiple comparisons when you’re comparing multiple groups. In addition, p values are further corrected using the Benjamini-Hochberg (FDR) adjustment.

Image of volcano plot dashboard in Ometa Flow, including volcano plot, boxplot, and result table. — *Volcano Plot Dashboard in Ometa Flow. Data shown is publicly available (MSV000086989).*

In the top left, you’ll notice the option to display raw or FDR-adjusted p values. The raw results are already adjusted using Tukey’s HSD but don’t include the FDR adjustment. You’re also able to display boxplots of specific metabolites of interest, which allows you to make informed decisions without simply relying on fold change and p value cutoffs.

*In this context, a real difference is one that’s due to biology and not just random chance.

**This is assuming you’re using the right statistical test for your data. If you’re using the wrong test, that p value means nothing.

Statistics: p values

Further Reading:

Statistics: p values

Further Reading:

Statistics: the basics

Statistics: normalization